행복을 담는 블로그
[Java / 자료구조] 그래프(Graph) 본문
💡그래프(Graph)란?
: 정점(Vertex)와 간선(Edge)의 집합

그래프 특징
- 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계 표현
- 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료구조
- 선형 자료구조나 트리로 표현하기 어려운 M:N의 관계를 표현한 것
- V개의 정점을 가지는 그래프는 최대 V * (V-1) / 2 간선이 가능
그래프 종류
- 무향 그래프(Undirected Graph) & 유향 그래프(Directed Graph)
- 가중치 그래프 (Weighted Graph)
- 방향도 있으면서 가중치 그래프
- 순환 그래프 (Cycle Graph)
- 비 순환 방향 그래프 (DAG, Directed Acyclie Graph)
1. 무향 그래프(Undirected Graph) & 유향 그래프(Directed Graph)
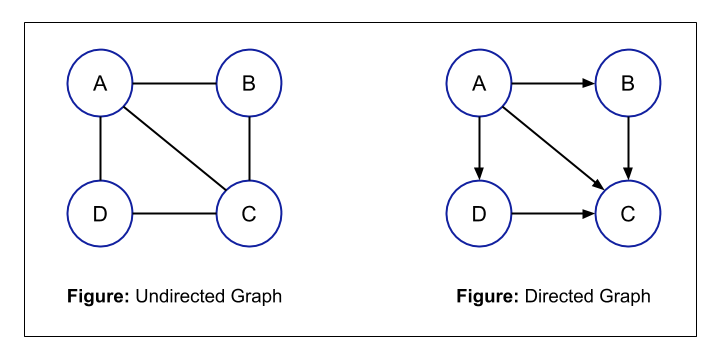
: 그래프의 간선에 방향성이 있고 없음의 차이
2. 가중치 그래프 (Weighted Graph)

: 정점과 정점을 잇는 간선에 가중치(비용)가 주어진 그래프
- 네트워크(Network) : 가중치 그래프 중 유향 그래프를 네트워크라고 한다.
- 각 정점들을 도시, 연결선을 도로라고 가정 => 가중치 : 각 도로를 지나기 위한 비용이나 도시 사이의 거리라고 생각할 수 있다.
- 가중치는 양수와 음수 모두 가능.
- 가중치의 합이 최소가 되는 최단 경로 문제는 경우에 따라 해결하는 알고리즘이 존재.
3. 순환 그래프 (Cycle Graph) v.s. 비순환 그래프 (Acyclie Graph)

1) 순환 그래프 (Cycle Graph)
: 그래프 내에서 하나 이상의 순환이 존재하는 그래프
방향성이 없는 그래프 (Undirected Graph)와 방향성이 있는 그래프(Directed Graph)가 존재
특징)
동일한 정점을 두 번 이상 방문할 수 있음
방향성이 없는 순환 그래프는 모든 정점이 서로 연결되어 닫힌 경로 형성
방향성이 있는 순환 그래프, 특정 정점들로 이루어진 서브 그래프가 순환 형성
2) 비순환 그래프(Acyclic Graph)
: 그래프 내에서 어떤 정점도 자신에게 다시 돌아오는 닫힌 경로를 형성하지 않는 그래프
- 방향성이 없는 그래프 (Undirected Acyclic Graph)
: 트리(Tree) 구조, Forest(포레스트 == 트리의 집합)라고 불림
- 방향성이 있는 그래프 (Directed Acyclic Graph, DAG)
: 위상 정렬이 가능, 모든 정점을 특정 순서로 나열할 수 있다. Acyclic Graph의 활용
1. Undirected Acyclic Graph (Tree/Forest)
- 네트워크 설계: 최소 비용 네트워크
- 데이터 구조: 이진 트리(Binary Tree), AVL 트리 등
- 경로 탐색 문제: 최단 경로, 최소 공통 조상(LCA)
2. Directed Acyclic Graph (DAG)
- 작업 순서 정리(Topological Sorting)
- 의존성 분석 (Dependency Resolution): 소프트웨어 빌드 시스템(Make, Gradle 등)
- 데이터 흐름 그래프: 컴파일러 중간 표현
- 그래프 알고리즘: 최단 경로(Dijkstra, Bellman-Ford)에서 사용참고) https://jackpot53.tistory.com/84
완전 그래프
- 모든 정점이 다른 정점들과 모두 연결 되어있는 그래프
- 간선의 개수 : V * (V-1) / 2
부분 그래프
- 일부 간선들을 가진 그래프
| 특성 | 완전 그래프 (Complete Graph) | 부분 그래프 (Subgraph) |
|---|---|---|
| 정의 | 모든 정점이 서로 연결된 그래프. | 주어진 그래프의 일부 정점과 간선으로 구성된 그래프. |
| 간선 개수 | 최대 간선을 가짐: (n 2) (무방향 그래프의 경우). | 원래 그래프의 간선보다 적음. |
| 연결성 | 항상 연결되어 있음. | 원래 그래프의 연결성과 무관. |
| 정점/간선 선택 | 모든 정점과 간선 포함. | 일부 정점과 간선 선택. |
| 사용 목적 | 모든 가능한 관계를 분석할 때 사용. | 특정 관심 영역만 분석하거나 그래프 단순화. |
그래프 경로
- 간선들을 순서대로 나열 한 것
- 하나의 정점을 한 번만 지나는 경로를 단순 경로
- 시작 정점에서 끝나는 경로를 사이클
그래프 표현 방법
- 인접 행렬 (Adjacent Matrix)
- 인접 리스트 (Adjacent List)
- 간선 배열 (Edge Array)
1. 인접 행렬 (Adjacent Matrix)

문제 ⇒ 정점의 번호가 0부터 시작, 1번부터 시작
두 정점을 연결하는 간선의 유무를 행렬로 표현
V * V개의 2차원 배열
행 번호와 열 번호는 그래프의 정점 번호
두 정점이 인접되어 있으면 1, 그렇지 않으면 0
무향 그래프 : 배열이 대칭된다.
유향 그래프
- 진출 차수 : 나로부터 나가는 노드
- 진입 차수 : 나로 들어오는 노드
public class AdjMatrix {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// V, E 의 갯수를 준다.
int V = sc.nextInt(); // 정점의 갯수(0 또는 1로 시작)
int E = sc.nextInt(); // 간선의 갯수
int[][] adjArr = new int[V][V]; // 만약 시작정점이 1이라면 [V+1][V+1]
for (int i = 0; i < E; i++) {
// 두 개의 정점이 주어진다.
int A = sc.nextInt();
int B = sc.nextInt();
// 가중치가 있다면, 값은 3개가 주어진다.
int W = sc.nextInt();
adjArr[A][B] = 1; // 가중치가 없다면 1을, 있다면 W를 저장하겠다. // 이 줄만 있다면 => 유향 그래프
adjArr[B][A] = 1; // 만약에 무향이라면, 반대의 경우도 같이 작성해주어야 한다!!
// adjArr[A][B] = adjArr[A][B] = W; // 한 줄 작성 가능
} // E개의 간선을 입력 받을 반복문
}
}
2. 인접 리스트 (Adjacent List)

public class AdjList {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// V, E 의 갯수를 준다.
int V = sc.nextInt(); // 정점의 갯수(0 또는 1로 시작)
int E = sc.nextInt(); // 간선의 갯수
List<Integer>[] adjList = new ArrayList[V];
// 기본적으로 전부 생성을 해주어야 NullPointExeption이 뜨지 않는다.
for (int i = 0; i < V; i++) {
adjList[i] = new ArrayList<>();
}
for (int i = 0; i < E; i++) {
int A = sc.nextInt();
int B = sc.nextInt();
// 가중치를 같이 저장하고 싶다면, 1. 클래스로 노드를 정의해서 넣던지, 2. int[]를 이용해서 넣던지
adjList[A].add(B);
adjList[B].add(A);
}
} // main
}인접 행렬(Adjacent Matrix) v.s. 인접 리스트(Adjacent List)
1. 정점이 100만개, 간선은 100개일 경우, 인접 리스트가 더 메모리 공간적으로 효율적 / 인접 행렬을 비어 있는 공간이 너무 많다.
2. A와 B가 인접하냐? 라는 것을 알아보기 위해서는 인접 행렬이 더 효율적 / 인접 리스트를 쓸 경우, 서로 인접한지를 알기 위해서 타고타고 가서 확인해보아야 한다.
| 특성 | 인접 행렬 (Adjacency Matrix) | 인접 리스트 (Adjacency List) |
|---|---|---|
| 구조 | 2차원 배열 | 정점마다 연결된 정점의 리스트 |
| 공간 복잡도 | O(n^2) | O(V + E) |
| 간선 존재 확인 | O(1) | O(degree(i)) ((i)의 차수에 비례) |
| 간선 추가/삭제 | O(1) | O(1) |
| 메모리 효율 | 비효율적 (희소 그래프에서 공간 낭비) | 효율적 (희소 그래프에 적합) |
| 구현 복잡도 | 구현 간단 | 구현 상대적으로 복잡 |
| 적합한 그래프 유형 | 밀집 그래프 (Dense Graph) / 빠르게 간선 존재 여부를 확인 해야하는 경우 | 희소 그래프 (Sparse Graph) / 그래프 탐색(DFS, BFS)에 유리 |
3. 간선 배열(Edge Array)
: 다양한 방법을 활용하여 간선 배열을 만들 수 있다.
주로 Edge라는 클래스를 만들어 Edge[] 배열을 만드는 방법을 가장 많이 사용하는 것 같다.
public class EdgeArray {
static class Edge {
int A, B, W; // 시작, 끝, 가중치 저장
public Edge(int a, int b, int w) {
super();
A = a;
B = b;
W = w;
}
@Override
public String toString() {
return "Edge [A=" + A + ", B=" + B + ", W=" + W + "]";
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// V, E 의 갯수를 준다.
int V = sc.nextInt(); // 정점의 갯수(0 또는 1로 시작)
int E = sc.nextInt(); // 간선의 갯수
// 1. 객체 배열 만들어서 간선 배열 활용
Edge[] edges = new Edge[E]; // 객체 배열
for (int i = 0; i > E; i++) {
int A = sc.nextInt();
int B = sc.nextInt();
int W = sc.nextInt();
edges[i] = new Edge(A, B, W);
}
///////////////////////////////////////
// 2. 리스트를 활용하는 방법
List<Edge> edges2 = new ArrayList<>();
for (int i = 0; i < E; i++) {
edges2.add(new Edge(sc.nextInt(), sc.nextInt(), sc.nextInt()));
}
//////////////////////////////////////
// 굳이 객체까지 만들어야 하나?
// 3. 이차원 배열 활용하는 방법
int[][] edges3 = new int[E][3]; // 0 : 시작, 1 : 끝, 2 : 가중치
for (int i = 0; i < E; i++) {
int A = sc.nextInt();
int B = sc.nextInt();
int W = sc.nextInt();
edges3[i][0] = A; // 시작 정점
edges3[i][1] = B; // 도착 정점
edges3[i][2] = W; // 가중치
}
} // main
}출처)
https://afteracademy.com/blog/introduction-to-graph-in-programming/
'BackEnd > Java' 카테고리의 다른 글
| [Java / 자료구조] 트리(Tree) (0) | 2024.12.23 |
|---|---|
| [Java / 자료구조] Array v.s. LinkedList (0) | 2024.12.11 |
| [Java] int 와 long 데이터 타입 크기 / 백준 2420번 (0) | 2024.07.12 |
| [Java] Scanner() 로 input 값 입력 받기 (0) | 2024.07.11 |



